"In the land of the blind, the one-eyed man is king"
Twonker
Facebook

See "The Twonker - A Brief Introduction" for an overview.

Overtones

When a length of string (or a column of air) is made to vibrate it produces a pitch, which is called the Fundamental.

While the string is vibrating at the Fundamental frequency, the string also vibrates at another frequency half the size of the Fundamental, and another at one-third, and another at one-quarter, and so on indefinitely.

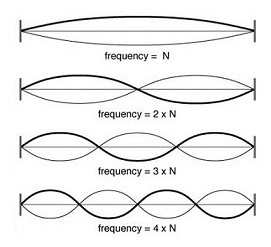
This is one way to visualize the Fundamental and the first three Overtones from the Series. The Fundamental is represented at the top, and each successive overtone moving down-wards is visualized with respect to it's relative frequency with the Fundamental.

Each individual frequency is vibrating with all the others at the same time. All musical instruments generate the same pattern of overtones. However, different instruments will accentuate and lessen different overtones in their respective series. This is why a clarinet sounds different from a flute when they play the same tone at the same volume. The difference is in the relative volumes of their Overtone Series.

Let's use a Fundamental frequency of 100 Hz as a convenient example. When 100 Hz is produced by a vibrating string, the first six tones in the Overtone Series are:

Each overtone is an exact multiple of the Fundamental at 100 Hz.

Closest Piano Key
Overtone Freq Freq Note Difference
Fundamental 110 Hz 110 Hz A2 None
1st Overtone 220 Hz 220 Hz A3 None
2nd Overtone 330 Hz 329.6 Hz E4 -2 cents
3rd Overtone 440 Hz 440 Hz A4 None
4th Overtone 550 Hz 554.4 Hz C#5 +14 cents
5th Overtone 660 Hz 659.3 Hz E5 -2 cents

A Practical Example

Now let's use "A2" (110 Hz) and map out the first six tones in order to compare them to the frequencies on a piano.

Looking at the Overtone Series in musical terms, the octave appears as the 1st and 3rd overtone. It's the only "perfect" interval when comparing the Overtone Series with the 12-tone system on the piano.

In music, the Perfect 5th is considered a very "stable" interval. The Overtone Series contains a tone that's very close to a Perfect 5th; but it's not an exact match. The common Perfect 5th is 2 cents flat.

The Modern Scale's origins in the Overtone Series

There are studies that show how the modern 12-tone system is derived from the Overtone Series (see Paul Hindemith's, "The Craft of Musical Composition: Book 1 - Theoretical Part". ISBN 0901938300; Chapter II.5 "Paths to Scale Formation"). In actuality, only the First Overtone is found in the modern 12-tone system (the octave!).

The other tones in our modern system have been "approximated" by simply dividing the octave into twelve equal intervals. This is known as Equal Temperament ("ET"). When we divide the octave into twelve equal intervals and compare with the Overtone Series we see some interesting correlations (keeping in mind 1,200 cents is one octave; each half-step measuring 100 cents):

All the Overtones that the Twonker makes accessible are found within the first 26 Overtones in the series. The Twonker maps 15 unique Overtones over each Fundamental. Since a piano only has 12 keys per octave, accessing all 15 overtones presents a problem.

The following intervals have two possible Overtones to choose from: The Diminished 5th, minor 6th, minor 7th and Major 7th. For these intervals, only one of the two Overtones are accessible at a time. The Overtone that's encountered earlier in the Overtone Series is chosen by default for these intervals.

In practical terms, let's assume the Fundamental is "C", and the player plays the Normal Tone "E". The interval between C and E is a Major 3rd. The default Alteration for the Major 3rd is +14 cents. The Twonker translates the Normal Tone into a Twonked Tone and Pitchbends it 14 cents sharp.

Further Reading